Training@Staburo: Multiple Imputation
Multiple Imputation (MI) is a technique to replace missing data with substituted values. The promise of this method is to estimate less biased estimates compared to state-of-the-art methods like Last Observation Carried Forward (LOCF).
In a MI approach, the same missing value is imputed multiple times in order to reduce noise in contrast to single imputation.
The introduced implementation is especially suited for the MI of longitudinal data. The approach utilizes the longitudinal information of the data to further minimize the prediction error of the imputation process.
Two step process for longitudinal data
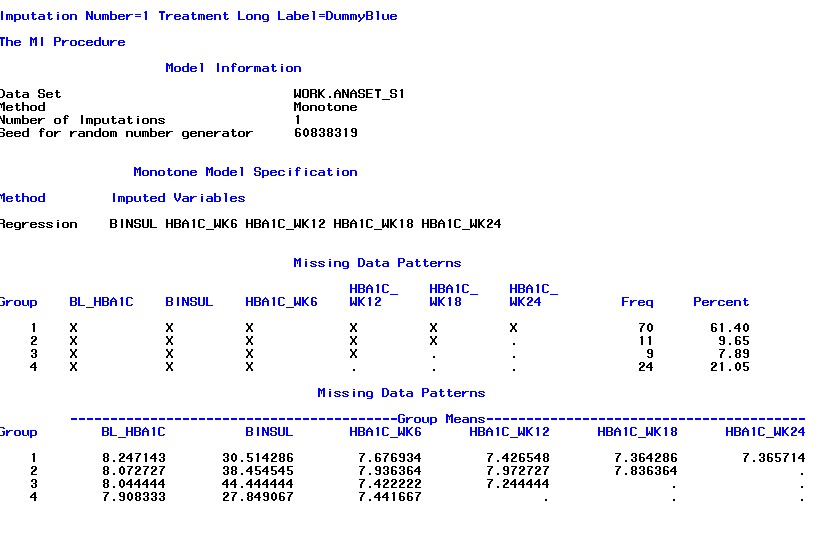
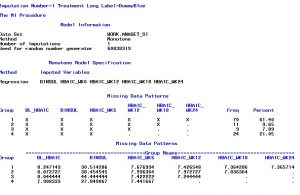
The implementation is realized by a two step process. The first MI step serves as input for the second MI step. Step 1 uses an EM algorithm to impute the data until a monotone missing pattern is achieved. Monotone missing is achieved if the sequence of longitudinal information does not contain any “holes”. A hole is hereby a missing value between observed values, assuming a chronologic order in a longitudinal setting. This process is repeated m-times to get multiple imputations. The second step can utilize multiple prediction algorithms, e.g. regression, predictive mean matching or propensity score. However, the underlying process is always the same. Every remaining missing value is now predicted from the information that occurs earlier in the chronologically sequence.
After the imputation, the statistical analysis is done separately for every imputation dataset and the results are pooled according to Rubin’s Rules.
The talk discussed the practical implementation in SAS with proc MI.

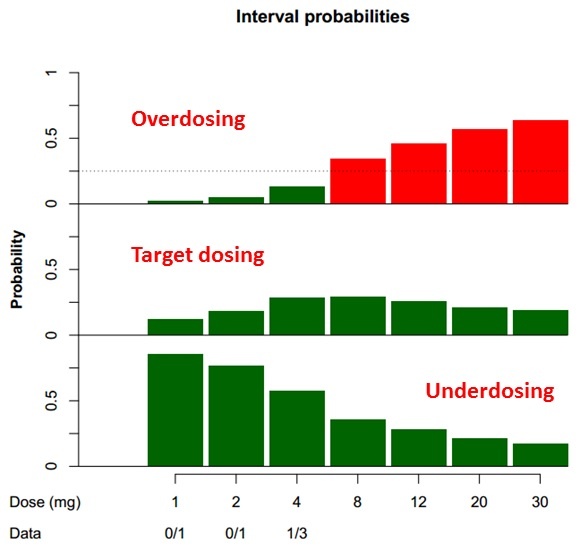
 In the past few years, more and more articles dealing with Bayesian statistics and Bayesian designs in clinical trials were published. Such designs are being developed especially for clinical trials with small number of patients, where it is crucial to get the most information from the limited available data.
In the past few years, more and more articles dealing with Bayesian statistics and Bayesian designs in clinical trials were published. Such designs are being developed especially for clinical trials with small number of patients, where it is crucial to get the most information from the limited available data.
Recent Comments